方格取数问题(二分图+建模技巧)
将原图黑白染色,并保证产生矛盾的两个位置颜色不同。源点连接黑点,白点连接汇点,黑点连接与之产生矛盾的白点。通过 最大和=全局和-最小割,在建立的网络上跑最小割(最大流)即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21for(register int i=1;i<=M;++i){
for(register int j=1;j<=N;++j){
int w;
scanf("%d",&w);
sum+=w;
if((i+j)&1){
AddEdge(S,(i-1)*N+j,w);
AddEdge((i-1)*N+j,S,INF);
for(register int k=0;k<=3;++k){
int tx=i+nx[k],ty=j+ny[k];
if(tx<1||tx>M||ty<1||ty>N) continue;
AddEdge((i-1)*N+j,(tx-1)*N+ty,INF);
AddEdge((tx-1)*N+ty,(i-1)*N+j,0);
}
}
else{
AddEdge((i-1)*N+j,T,w);
AddEdge(T,(i-1)*N+j,INF);
}
}
}
题目列表-网络流
公告 2019-03-24
2019/3/24,tth37搭建了这个github博客。
tth37希望在这个博客里记录一些自己学习OI的心得,并发布一些题解,贴出学习规划。
但tth37实在是太弱了,因此他会更新得十分缓慢。
另外,还请shiwt巨佬多多指教。
任何一个伟大的思想,都有一个微不足道的开始。
p.s. 可能会将洛谷博客上的文章搬运过来,所以有些文章的发布时间可能在此之前,请别见怪。
题目列表-动态规划
任务安排(斜率优化+费用提前计算)
$$
f[i]=min_{0\le j<i}{f[j]-(S+T[i])*C[i]+T[i]*C[i]+S*C[N]}
$$
特别行动队(斜率优化)
$$
f[i]=max_{0\le j<i}{f[j]+A*(S[i]-S[j])^2+B*(S[i]-S[j])+C}
$$
玩具装箱(斜率优化)
$$
f[i]=min_{0\le j<i}{f[j]+(A[i]-A[j]-L-1)^2}
$$
斜率优化的适用范围是只有一个自变量。形如这样的转移方程:
$$
f[i]=min_{0\le j<i}{f[j]+(i-j+S[i]-S[j]-L-1)^2}
$$操作难度较大,可以将$S[i]+i$存在$A$数组中,即可全部化为一个自变量。
锯木厂选址(斜率优化)
$$
f[i]=min_{1\le j<i}{C[i-1]-W[j]*(D[i]-D[j])}
$$
打印文章(斜率优化)
$$
f[i]=min_{0\le j<i}{f[j]+(S[i]-S[j])^2+M}
$$
调到心态爆炸……getK函数中如果除数为0则要返回1e100
序列分割(斜率优化)
$$
f[i][j]=max_{0 \le k<j}{f[i-1][k]+S[k]*(S[j]-S[k])}
$$
不开long long见祖宗。题目中如果说“非负整数”一定记得判断除数是否为0。对于转移方程中的第一维,稍加观察就会发现可以使用滚动数组。(虽然也需要一些额外的数组记录状态)
绿色通道(二分答案+单调队列)
$$
f[i]=min_{i-M-1 \le j <i}{f[j]+a[i]}
$$
二分发怒程度$M$,$f$数组中存储选择当前题目最少多少体力。统计最终答案只需检验最后$M$个状态即可。
1 | int ans=INF; |
股票交易(单调队列+很多条件)
$$
f[i][j]=-AP[i]*j(0 \le j \le AS[i])
$$$$
f[i][j]=max{f[i][j],f[i-1][j]}(0 \le j \le M)
$$$$
f[i][j]=max_{j-AS[i] \le k<j}{f[i-W-1][k]-(j-k)*AP[i]}(0 \le j \le M)
$$$$
f[i][j]=max_{j<k \le j+BS[i]}{f[i-W-1][k]+(k-j)*BP[i]}(0 \le j \le M)
$$
条件特别多,需要仔细分析题意并且列出状态转移方程。先进行较简单的转移,再利用单调队列进行复杂转移。注意第四种状态转移要使用逆序循环。如此恶心的状态转移让我不禁想起飞扬的小鸟
潜入行动(背包类树形dp)
$$
f[u][i+j][0][0]=\sum f[u][i][0][0]*f[v][j][0][1]
$$$$
f[u][i+j][1][0]=\sum f[u][i][1][0]*(f[v][j][0][0]+f[v][j][0][1])
$$$$
f[u][i+j][0][1]=\sum (f[u][i][0][1]*(f[v][j][0][1]+f[v][j][1][1])+f[u][i][0][0]*f[v][j][1][1]
$$$$
f[u][i+j][1][1]=\sum (f[u][i][1][0]*(f[v][j][1][0]+f[v][j][1][1])+f[u][i][1][1]*(f[v][j][0][0]+f[v][j][0][1]+f[v][j][1][0]+f[v][j][1][1]))
$$特别注意空间问题,中间运算转
long long,保存时再转int
子串(线性dp+滚动数组)
$$
f[i][0][0][0]=1
$$$$
f[i][j][k][0]=f[i-1][j][k][0]+f[i-1][j][k][1]
$$$$
a[i]=b[j]:f[i][j][k][1]=f[i-1][j-1][k][1]+f[i-1][j-1][k-1][0]+f[i-1][j-1][k-1][1]
$$$$
a[i] \ne b[j]:f[i][j][k][1]=0
$$滚动数组注意点:
- 状态转移方程只依赖前一维或前两维状态
- 状态数组要被滚动的一维只开1或2
- 对于0/1滚动数组,可以结合位运算
&和^进行判断奇偶性和减一操作
换教室(期望dp)
$$
f[i][j][0]=min{f[i-1][j][0]+dis[C[i-1]][C[i]],f[i-1][j][1]+K[i-1]*dis[D[i-1]][C[i]]+(1-K[i-1])*dis[C[i-1]][C[i]]}
$$$$
f[i][j][1]=min{f[i-1][j-1][0]+K[i]*dis[C[i-1]][D[i]]+(1-K[i])*dis[C[i-1]][C[i]],f[i-1][j-1][1]+K[i-1]*K[i]*dis[D[i-1]][D[i]]+K[i-1]*(1-K[i])*dis[D[i-1]][C[i]]+(1-K[i-1])*K[i]*dis[C[i-1]][D[i]]+(1-K[i-1])*(1-K[i])*dis[C[i-1]][C[i]]}
$$期望dp可以单独开一维表示状态,以便于列举出所有情况。本题的转移方程是一个很好的例子。
如果tth37开心的话,Ta可能会写一篇数学期望专题具体讲解此类题目。
过河(线性dp+玄学离散化)
$$
f[i]=min_{S \le j \le T}{f[i-j]+flag[i]}
$$由于m非常小,因此采用2520缩点,即两点之间距离超过2520的,可以将距离改为$dis % 2520$,从而离散化。
统计单词个数(线性dp+字符串)
$$
f[i][j]=max{f[i][j],f[r][j-1]+g[r+1][i]}
$$字符串处理使用string类find函数。
线性dp时再次强调,需要分清阶段、状态和决策变量;阶段在最外层循环,决策在最内层。在寻找关系时可以从推导或定义角度辨析,也可以根据转移方程进行识别。
棋盘制作(单调栈)
似乎没有转移方程
注意单调栈的处理方式(玄学方法或通用方法),在退栈时务必退干净。
1 | //玄学方法: |
题解-luogu-p1022计算器的改良
本题是一道非常漂亮的模拟。只要能理清思路,代码并不会特别复杂。
首先分析题目。解一元一次方程最简单的方法就是移项,把常数移到等号右侧,把一次项系数移到等号左侧,用常数除以系数即为答案。那么在读入字符串的过程中,便可以进行操作。
对于字符串中的数据,我们可以用类似快读的方法读入。然而,要判断这些数据从哪里来,到哪里去,便是本题的关键所在。
对于每个数据,要想清楚地辨别它的身份,我们只需解决三个问题:
1.该数据是正数还是负数?
3.该数据在等号左侧还是在等号右侧?
2.该数据是常数还是系数?
第一个问题看似十分无脑,用一个变量f1来存储符号即可(将f1赋值为1或-1,在读入数据结束时将得到的数据乘以f1)。但需特别注意,在一个表达式的开头(等号左侧和等号右侧的表达式)不会有‘+’、‘-’符号,所以在程序的开头和读入‘=’号是,要将f1赋值为1。
第二个问题也非常简单,可以用变量f2来存储。因为这个问题与移项运算的符号有关,因此也可以将f2赋值为1或-1,并约定在等号左侧时f2为1,在等号右侧时f2为-1。(当然你也可以反着约定)
第三个问题同样不难解决。在读入数据结束后(即读入了一个符号),判断这个符号是运算符还是字母即可。如果是字母,则将得到的数据移到等号右侧,否则将数据移到等号左侧。但是还有一个注意点:如果一个未知数的系数为1,我们会将系数省略。因此在读入数据为0时,我们要将其更改为1。
经过分析,你会发现本题一点也不难实现。其关键在于对数据状态的准确描述。用清晰、简洁的变量描述状态,根据不同的状态采取不同的措施,这便是编程学习的一大基本素养。
代码如下:
题解-luogu-p1204挤牛奶
介绍一种本题的贪心解法。
本题要求读入一些挤牛奶的时间段,求最长至少有一人在挤牛奶的时间段和最长没有人在挤牛奶的时间段。把读入的区间视作线段,则题意转变为求至少有一条线段覆盖的最大区间和没有线段覆盖的区间。
假设读入数据如下: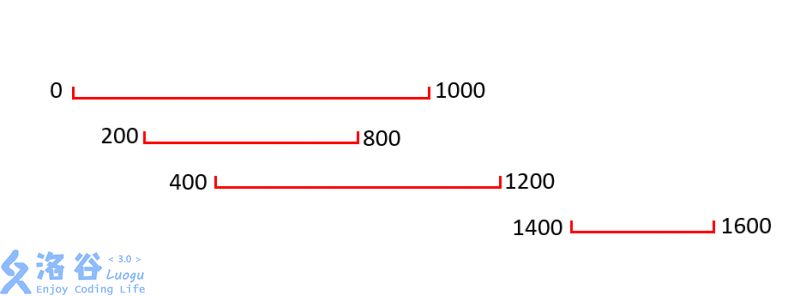
首先按照4条线段的起点位置排序(具体原因后面解释)。将begin设置为第一条线段的起点,将end设置为第一条线段的终点。
然后从第二条线段开始判断。如果该线段的起点小于end,则说明这两条线段有重合部分,将end更新为max{end,该线段的终点位置}。如果该线段的起点大于end,则说明该线段及以后的线段再也不会与前面的线段产生任何重合部分(这也就是排序的作用),那么可以更新ans1和ans2的值:ans1更新为max{ans1,end-begin},ans2更新为max{ans2,该线段的起点位置-end}。具体参见图中第4条线段,ans1被更新为1200-0,ans2被更新为1400-1200。
程序已经基本成型,但要注意在输出答案前更新一遍ans1的值,这是为了避免所有线段均有重合部分而无法判断的情况。另外,ans1和ans2要初始化为0。
程序如下: