题目链接

给定一个长度为$n$的数组$a$，取$k$个各不相同的连续区间$[l,r]$ 使得这些区间所有元素的异或和的和最大，求这个最大值
（$ 1 \le n \le 5 \times 10^5,1\le k \le min(\frac{n(n-1)}{2},2\times 10^5),0\le a_i \le 4294967295$）

感谢@oy的贡献

tth37 Blog已经绑定了最新域名：tth37.cn ！(购买自阿里云)

由于一些奇怪的原因（DNS域名解析和CNAME配置问题），我的博客在四月七日至四月八日出现许多异常，现已全部修复。

但在四月九日至四月十日的测试中，我被疯狂打脸；现在已经可以保证，只要在浏览器输入栏输入 tth37.cn，即可自动跳转https://tth37.cn，并在*CloudFlare*证书授权下安全运行。

请大佬们在新域名下体验高速加载和流畅访问新体验吧！

另外，左侧边栏“日程表”已经启用；网站基本搭建完毕。以后将缩减网站维护时间。

概述

可持久化数据结构可以存储数据集在任意时间的历史状态。“可持久化”的基本思想是在每项操作结束后，仅创建数据结构中发生改变的部分的副本，不拷贝其他部分。这样一来，维护数据结构的时间复杂度没有增加，空间复杂度仅增长为与时间同级的规模。换言之，可持久化数据结构能够高效地记录一个数据结构的所有历史状态。

这是一个并不简单的背包类树形dp……

很自然地想到状态定义：$f[u][k][0/1][0/1]$表示以$u$为根的子树中，总共选择$k$个结点，其中除了$u$以外的所有结点均被监听到，$u$结点选或不选，$u$结点是否被覆盖的情况下，一共有多少种方案。

状态转移看似十分麻烦。每个结点$u$都有许多子结点，很难统计出每个子结点的所有情况（似乎在组合数学的范畴）。但是我们可以用十分巧妙的树形背包来进行状态转移。树上背包的转移套路是：

$$
f[u][i+j]=combine(f[u][i],f[v][j])
$$

相当于每递归访问完一个子结点，就把子节点上的状态与当前已经处理的状态一一配对，保证不重不漏且兼顾效率。具体的转移方程为：

$$
f[u][i+j][0][0]=\sum f[u][i][0][0]*f[v][j][0][1]
$$

$$
f[u][i+j][1][0]=\sum f[u][i][1][0]*(f[v][j][0][0]+f[v][j][0][1])
$$

$$
f[u][i+j][0][1]=\sum (f[u][i][0][1]*(f[v][j][0][1]+f[v][j][1][1])+f[u][i][0][0]*f[v][j][1][1]
$$

$$
f[u][i+j][1][1]=\sum (f[u][i][1][0]*(f[v][j][1][0]+f[v][j][1][1])+f[u][i][1][1]*(f[v][j][0][0]+f[v][j][0][1]+f[v][j][1][0]+f[v][j][1][1]))
$$

具体实现时还应注意：因为阶段（即扫描子结点个数）的划分，在每次转移前都要先记录原始的$u$结点上的数据，否则会导致混乱。

写的不好！计划重写一篇。

树形背包博大精深！

绝对不咕！

题目链接

不难发现，每个方格会与其上下左右四个方格产生矛盾。编程的任务即找到一种不产生矛盾的选择方案，并且使得取出的数总和最大。

首先对图进行黑白染色，目的是使产生矛盾的两个位置分别位于不同的色块中，方便建图。

源点与所有白色位置相连，权值为该位置上的数字；所有黑色位置与汇点相连，权值也为该位置上的数字；所有白色位置与其上下左右（注意边界情况）的黑色位置相连，权值为无穷大。

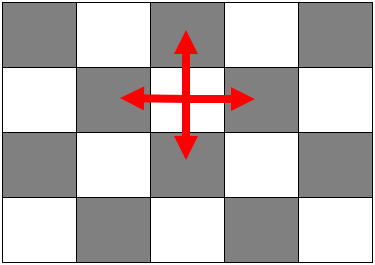
如此建图后，可以发现存在源点到汇点的增广路，这也意味着原图中存在产生矛盾的两个位置。假设一开始选取M*N网格中的所有方块，我们的任务是割掉网络中的一些边（即删去一些方块），使得割去的边权最小。割去网络中的边就相当于删掉两个矛盾位置中的其中一个，因此当网络中不再有源点到汇点的增广路，就意味着矛盾全部消除。

问题便转化为求解最小割（最大流）的问题。输出答案为全局和减去最小割。