Summarize
有 $n$ 种药,每种药由若干药材组成,恰好有 $n$ 种不同的药材。要求选出 $k$ 种药,并且使用的药材并集大小也为 $k$,使得药材的权值和最小。
$n \le 300$
不难发现,每个方格会与其上下左右四个方格产生矛盾。编程的任务即找到一种不产生矛盾的选择方案,并且使得取出的数总和最大。
首先对图进行黑白染色,目的是使产生矛盾的两个位置分别位于不同的色块中,方便建图。

源点与所有白色位置相连,权值为该位置上的数字;所有黑色位置与汇点相连,权值也为该位置上的数字;所有白色位置与其上下左右(注意边界情况)的黑色位置相连,权值为无穷大。
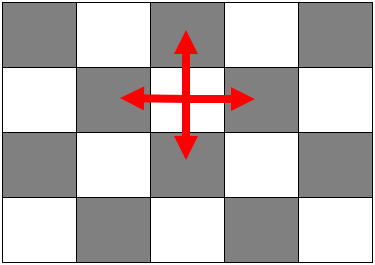
如此建图后,可以发现存在源点到汇点的增广路,这也意味着原图中存在产生矛盾的两个位置。假设一开始选取M*N网格中的所有方块,我们的任务是割掉网络中的一些边(即删去一些方块),使得割去的边权最小。割去网络中的边就相当于删掉两个矛盾位置中的其中一个,因此当网络中不再有源点到汇点的增广路,就意味着矛盾全部消除。
问题便转化为求解最小割(最大流)的问题。输出答案为全局和减去最小割。
Update your browser to view this website correctly. Update my browser now