扩展 KMP

本文源自计蒜客课件，切勿外传！

扩展 KMP 能在 $O(|S|+|T|)$ 时间复杂度内处理出字符串 $S$ 的所有后缀与字符串 $T$ 的最长公共前缀。

之所以称为扩展 KMP，是因为其思想和 KMP 算法很类似。

$\text{next}$ 函数

记 $\text{next}[i]$ 表示后缀 $i$ 即 $T[i..|T|]$ 与 $T$ 的最长公共前缀。

例如：

注意 $\text{next}$ 数组是对于 模式串 $T$ 构建的。

如何获取 $\text{next}$ 函数

假设 $\text{next}[i](0\le i<x)$ 的值都已经求出，现在要求 $\text{next}[x]$。

假设 $p=\max\lbrace i+\text{next}[i]-1\rbrace$ 对于所有 $0< i < x$，我们找到 $i+next[i]-1$ 的最大值，令 $k$ 为这个最大值对应的 $i$，令 $p$ 为 $k+\text{next}[k]-1$，$p$ 就是我们目前已知的匹配到的最远位置。

根据定义我们可以得到： $T[k..p]=T[0..\text{next}[k]-1]$，如下图所示蓝色部分：

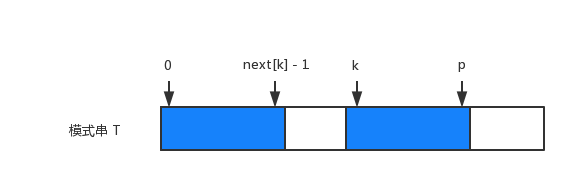
现在我们要求 $T[x..n-1]$ 与 $T[0..n-1]$ 的最长公共前缀。

由 $T[k..p]=T[0..\text{next}[k]-1]$ 得：

$T[x..p]=T[x-k..\text{next}[k]-1]$，如下图所示红色部分：

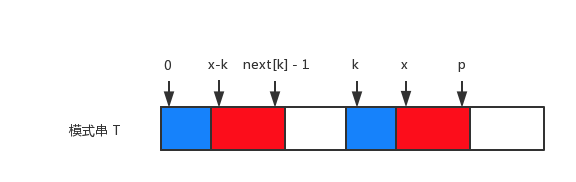
设 $l=\text{next}[x-k]$，根据下图，可以得到：

$T[0..l-1]=T[x-k..x-k+l-1]=T[x..x+l-1]$，如下图所示黄色部分：

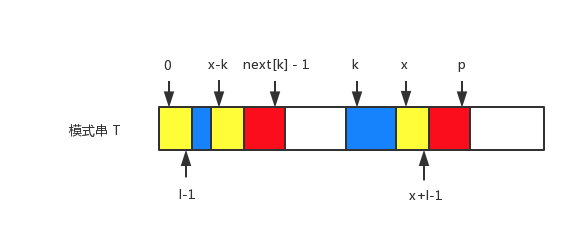
也就是说，如果图中黄色部分小于红色部分，也就是 $l<p-x+1$ 即 $x+l\le p$，那么我们可以确定 $\text{next}[x]=l$。否则，我们从 $p-x+1$ 和 $p+1$ 位置开始逐一比较，求出 $\text{next}[x]$ 的值。

由于在这个过程中， $p$ 满足不下降性质，因此总体时间复杂度为 $O(n)$。

获取 $\text{next}$ 函数的代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

void exKMP_pre(char *T) {
    int n = strlen(T);
    next[0] = n;
    int p = 0;
    while (p + 1 < n && T[p] == T[p + 1]) p++;
    next[1] = p;
    int k = 1;
    for (int x = 2; x < n; ++x) {
        p = k + next[k] - 1;
        int l = next[x - k];
        if (x + l <= p) next[x] = l;
        else {
            int j = p - x + 1;
            if (j < 0) j = 0;
            while (x + j < n && T[x + j] == T[j]) j++;
            next[x] = j;
            k = x;
        }
    }
}

解决原问题

记 $\text{extend}[i]$ 表示字符串 $S$ 的第 $i$ 个后缀和 $T$ 的最长公共前缀。假设 $\text{extend}[i](0\le i<x)$ 已经求出，现在需要计算 $\text{extend}[x]$。

已知：$S[k..p]=T[0..\text{extend}[k]]$，求 $S[x..n]$ 与 $T[0..m]$ 的最长公共前缀。解法与计算 $\text{next}$ 的方法类似，记录 $p=i+\text{extend[i]}-1$ 的最大值。

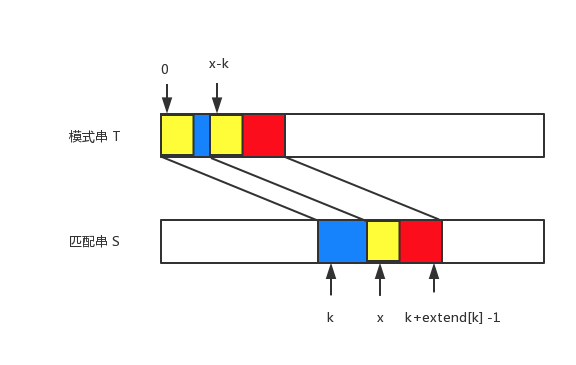
根据红色部分的等价，我们可以利用 $\text{next}[x-k]$ 得到黄色部分等价性，剩下的分析就和求 $\text{next}$ 的过程一样了。

获取 $\text{extend}$ 函数的代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

void exKMP(char *S, char *T) {
    int n = strlen(T), m = strlen(S);
    int p = 0;
    while (p < m && p < n && S[p] == T[p]) p++;
    extend[0] = p;
    int k = 0;
    for (int x = 1; x < m; ++x) {
        p = k + extend[k] - 1;
        int l = next[x - k];
        if (x + l <= p) extend[x] = l;
        else {
            int j = p - x + 1;
            if (j < 0) j = 0;
            while (x + j < m && j < n && S[x + j] == T[j]) j++;
            extend[x] = j;
            k = x;
        }
    }
}