现在我随机@一个人 这个人必须帮我写题目概括
@xj
这是一篇虚树入门题解。
考虑题目中 $m=1$ 的情况。树上动规,定义状态 $f[u]$ 表示切断节点 $u$ 与该子树内所有关键点的路径,最小总代价。状态转移方程如下:
$$
f[u]=
\begin{equation}
\begin{cases}
w(u,v) \ \texttt{if h[v]=1} \
\min(w(u,v),f[v])\ \texttt{if h[v]=0}
\end{cases}
\end{equation}
$$
动态规划部分不再赘述。该算法复杂度为 $O(n)$ 。
考虑题目中 $m\not= 1$ 的情况。如果对于每一次查询,都进行一次 $O(n)$ 复杂度的遍历显然无法接受。观察到题目中 $\Sigma{k}$ 的取值不大,可以考虑针对没个询问,舍弃树上的一些非关键点,仅保留一棵包含原树上部分节点的虚树,并在虚树上进行动态规划。
那么,在虚树上应该保留原树上的哪些点呢?
首先,每次讯问中给出的 $k$ 个关键点(资源丰富的岛屿)显然应该包含在虚树中。其次,任意两个关键点的最近公共祖先也应该包含在虚树中;因为在本题中,切断一条边可以同时切断根节点与多个关键点间的路径,最近公共祖先的存在为动态规划提供了这种状态转移。最后为了方便,我们可以将 $1$ 号节点(即根节点)也加入到虚树中。
构造虚树的方法很多,在这里介绍一种用栈建树的算法流程。
令 $1$ 号节点为虚树的根。
将所有关键点按照其在原树中的 dfs 序升序排序。假设当前正在处理的关键点为 $u$ 。
维护一个栈,使得栈底到栈顶的元素依次为虚树上从根节点到节点 $u$ 的一条链。
这里为什么要维护一个栈呢?
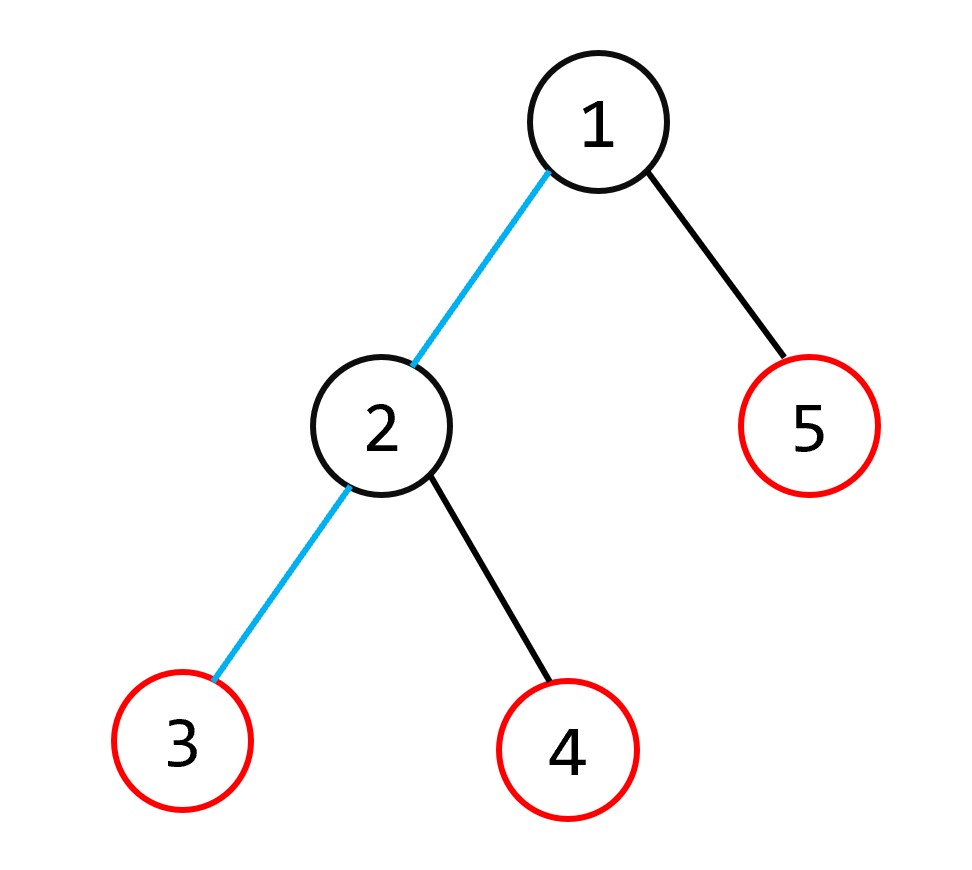
如图:在处理完 $3$ 号关键点后,虚树中只有 $1$ 、 $3$ 两个节点,栈中的元素依次为 $1$ 、 $3$ 。但是这条链是不完整的,可以观察到在处理 $4$ 号关键点时,还需要将 $2$ 号节点添加到虚树中。利用栈的性质,我们可以动态维护一条虚树上的链,并在必要的时候添加节点。
回到刚才的叙述,当前正在处理关键点 $u$ 。根据栈的定义,上一个处理的关键点一定为 $stack.top()$ 。
由于进行过排序,即节点 $u$ 的 dfs 序大于上一个关键点的 dfs 序,因此节点 $u$ 要么是上一个关键点的后代,要么与其没有祖先-后代的关系。
显然,如果节点 $u$ 是 $stack.top()$ 的后代,那么只需将节点 $u$ 入栈即可,因为 $u$ 在虚树中,一定是上一个关键点的儿子。
但是如果节点 $u$ 与 $stack.top()$ 没有祖先-后代的关系,那么此时的讨论将比较复杂。
可以结合上图观察,假设当前正在处理 $4$ 号关键点。我们可以首先将栈顶弹出,因为 $stack.top()$ 一定不在根节点到节点 $u$ 的链上。此时,栈中剩余的元素只有 $1$ 。然而, $3$ 与 $4$ 的最近公共祖先 $2$ 号节点还不在栈中;因此我们需要把 $2$ 号节点入栈,并将刚刚弹出的节点与新的栈顶在虚树中连边。处理结束后,将 $4$ 入栈。
接下来处理 $5$ 号关键点,此时栈中的元素依次为 $1$ 、$2$ 、$4$ 。首先将栈顶弹出,但由于我们接下来需要维护的链为 $1->5$ ,栈中仍然有节点 $2$ ,因此我们需要将 $2$ 和刚刚弹出的节点 $4$ 连边,并且重复以上操作。将新的栈顶 $2$ 弹出后,栈中只剩下节点 $1$ 。这时发现 $1$ 号节点恰好为 $5$ 与上一次处理的关键点 $4$ 的最近公共祖先,因此将 $1$ 与 $2$ 连边后,弹栈可以中止了。处理结束后,将 $5$ 入栈。
此时我们已经处理完了所有关键点,但是栈中的元素间还没有连边。将栈中的节点依次连边后,虚树的构建就完成了。
伪代码如下:
1 | 将关键点按照 dfs 序排序 |
可以证明,对于本题,虚树上的边权一定对应原树上两节点之间边权的最小值。证明不再赘述。
代码如下:
1 | #include <bits/stdc++.h> |