题目链接
介绍一种本题的贪心解法。
本题要求读入一些挤牛奶的时间段,求最长至少有一人在挤牛奶的时间段和最长没有人在挤牛奶的时间段。把读入的区间视作线段,则题意转变为求至少有一条线段覆盖的最大区间和没有线段覆盖的区间。
假设读入数据如下:
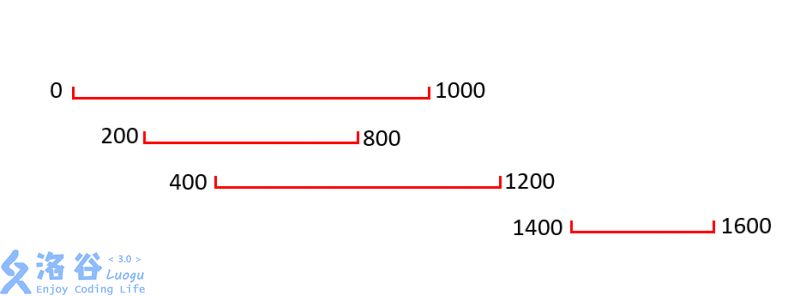
首先按照4条线段的起点位置排序(具体原因后面解释)。将begin设置为第一条线段的起点,将end设置为第一条线段的终点。
然后从第二条线段开始判断。如果该线段的起点小于end,则说明这两条线段有重合部分,将end更新为max{end,该线段的终点位置}。如果该线段的起点大于end,则说明该线段及以后的线段再也不会与前面的线段产生任何重合部分(这也就是排序的作用),那么可以更新ans1和ans2的值:ans1更新为max{ans1,end-begin},ans2更新为max{ans2,该线段的起点位置-end}。具体参见图中第4条线段,ans1被更新为1200-0,ans2被更新为1400-1200。
程序已经基本成型,但要注意在输出答案前更新一遍ans1的值,这是为了避免所有线段均有重合部分而无法判断的情况。另外,ans1和ans2要初始化为0。
程序如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| #include<bits/stdc++.h>
using namespace std;
int N;
struct node{
int begin,end;
}m[5005];
bool cmp(node a,node b){
return a.begin<b.begin;
}
int main(){
scanf("%d",&N);
for(register int i=1;i<=N;++i)
scanf("%d%d",&m[i].begin,&m[i].end);
sort(m+1,m+1+N,cmp);
int begin=m[1].begin;
int end=m[1].end;
int ans1=0,ans2=0;
for(register int i=2;i<=N;++i){
if(m[i].begin<=end)
end=max(end,m[i].end);
else{
ans1=max(ans1,end-begin);
ans2=max(ans2,m[i].begin-end);
begin=m[i].begin;
end=m[i].end;
}
}
ans1=max(ans1,end-begin);
printf("%d %d",ans1,ans2);
return 0;
}
|
